It is well-known that, historically, the availability of energy is highly related to economic growth in the long run. It is less clear whether this relationship should be expected to continue into the future, and it is also unclear whether energy causes economic growth, or whether growth causes increased energy consumption, or both.
Energy as a Factor in Growth
The Solow-Swan model of economic growth (Solow (1956) and Swan(1956)) holds that a nation’s economic growth can be expressed in terms of the total supply of labor and capital with the following Cobb-Douglas production function:
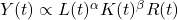 Solow-Swan growth model. Here Y, L, K, and R are total gross domestic product, labor, capital, and a residual term respectively. Each of these is expressed as a function of time t. The exponents α and β are to be estimated econometrically.
Solow-Swan growth model. Here Y, L, K, and R are total gross domestic product, labor, capital, and a residual term respectively. Each of these is expressed as a function of time t. The exponents α and β are to be estimated econometrically.
In the Solow-Swan model above, R(t) is a residual term that represents the deviation of actual gross domestic product from the value that is predicted from the stock of labor and capital. The additional assumption that α+β=1, also called constant returns to scale, is frequently made. In words, constant returns to scale imply that if the supplies of labor and capital are both multiplied by a value k, then total GDP will also be multiplied by k. Assuming constant returns to scale can result in residual terms that are quite large, necessitating additional explanatory factors for growth beyond labor and capital.
Ayres and Warr (2005) provide one such explanation in the form of energy for economic growth in the United States from 1900 to 1998. Moving away from the common Cobb-Douglas production function, they use a linear-exponential (LINEX) function that exhibits more complementarity between the factors of production, rather than mere substitutability. The LINEX function retains the property of constant returns to scale.
Ayres and Warr (2005) then consider how to measure energy. Data on American energy consumption is derived from the U.S. Federal Power Commission, the U.S. Department of Energy, and other sources. They consider two measures of energy. The first, denoted as E, is the heat content of fossil fuels, nuclear fuel, and wood, and the energy harnessed from hydroelectricity, wind, and solar. The second, denoted as B, is a more inclusive measure that entails the first form of energy, as well as potential work embodied in non-fuel wood, ores, and agricultural products. While B yields a slightly better fit than E, both perform poorly, as energy consumption, capital, and labor have all historically grown more slowly than the economy as a whole.
Ayres and Warr (2005) then consider a production production based on exergy, or the useful work performed by energy. These values, denoted as U_E and U_B, are obtained from B and E respectively by multiplying by thermodynamic conversion efficiency. Since efficiency has increased over time, U_E and U_B have grown faster than E and B. The authors find that these latter quantities, and U_B in particular, yield much better fits to the data than E and B.
Ayres and Warr (2005) find that with a LINEX production function with three factors–labor, capital, and U_B as defined above–the Solow-Swan residual largely disappears in modeling United States economic growth from 1900 to 1970. From 1970 to 1998, their last year of data, a small residual appears, though it is less than the residual with the common two-factor growth model. The authors offers two explanations for the residual after 1970. First, since its appearance roughly corresponds to the oil crises of the 1970s, it may represent the effect of conservation. Second, the residual may suggest the need for a fourth factor to represent the role of information technology. They nevertheless find that, despite the apparent decoupling of economic growth from energy consumption from the 1970s, there is still a strong relationship between the two quantities, and the relationship should be expected to remain well into the future.
Stern (2011) synthesizes traditional and ecological growth models and finds that historically, energy consumption has been a driver of economic growth. However, as energy’s share of economic output has decline, so too should the causative role of energy in economic growth. Stern argues that while an energy shortfall would negatively impact the world economy, an energy windfill in an economy that already experiences energy abundance would have comparatively little economic benefit.
Causation Between Energy and Growth
A weakness of Ayres and Warr (2005) is that, while it establishes a strong relationship between energy (exergy) consumption and economic growth in the United States in the 20th century, it does not establish causation. It remains unclear whether increased energy supplies cause economic growth, or whether a growing economy causes increased energy consumption, or if the causation flows both ways.
Granger causality, introduced in Granger (1969), is a statistical test of causality between two time series. The test works by identifying a correlation between the time series with a time lag. If a correlation is found between series A and series B with a time lag, then it is said that A Granger causes B. As illustrated by Maziarz (2015), the statistical test does not imply, in and of itself, epistomological causality between the time series, and unless a plausible causal mechanism between the two series is known from domain knowledge, genuine causality should not be assumed solely on the basis of the statistical test.
Tran et al. (2022) examine panel data of 26 countries of the Organisation for Economic Co-operation and Development–generally wealthy countries–of energy consumption and gross domestic product from 1971 to 2014. They find a threshold per-capita GDP of $48,170. Below that threshold, energy consumption is found to Granger cause gross domestic product. Above the threshold, the direction of causality reverses; in the long run, GDP is found to Granger cause energy consumption, while no such relationship is found in the short run. By comparison, per-capita GDP in the United States was just under $83,000 as of 2023. The results suggest that the importance of energy as a driver of economic growth diminishes for high levels of wealth.
Alola, Bekun, Sarkodie (2019) examine several variables related to ecological impact in 16 European Union countries from 1997 to 2014. They find that gross domestic product Granger causes nonrenewable energy consumption, but not the reverse. They also find a mutually causal relationship between renewable energy consumption and GDP.
Perera et al. (2024) consider the share of renewable and nonrenewable energy in a country’s mix, and they examine 152 countries with panel data cosisting of the share of renewable and nonrenewable energy and of gross domestic product. The countries are divided into four groups: developed, developing, least developed, and transitional. Among the four groups, the authors found that the share of renewable energy positively Granger causes economic growth in transitional countries (generally former republics of the Soviet Union), and no statistically significant relationship was found between the variables in the other country groups, as well as the world as a whole. The authors find that more statistically significant relationships hold for many individual countries.
The above results are not fully conclusive, but they do not give much reason to expect that an increase in energy consumption in wealthy countries will, in and of itself, cause an increase in gross domestic product.
References
Ayres, R. U., Warr, B. “Accounting for growth: the role of physical work”. Structural Change and Economic Dynamics 16(2), pp. 181-209. June 2005.
Solow, R.M. “A contribution to the theory of economic growth”. The Quarterly Journal of Economics 70(1), pp. 65-94. February 1956.
Swan, T.W. “Economic Growth and Capital Accumulation”. Economic Record 32(2), pp. 334-361. November 1956.
Tran, B. L., Chen, C. C., Tseng, W.C. “Causality between energy consumption and economic growth in the presence of GDP threshold effect: Evidence from OECD countries”. Energy 251:123902. July 2022.
Granger, C. W. J. “Investigating Causal Relations by Econometric Models and Cross-spectral Methods”. Econometrica 37(3), pp. 424-328. August 1969.
Maziarz, M. “A review of the Granger-causality fallacy”. The Journal of Philosophical Economics : Reflections on Economic and Social Issues VIII(2), pp. 86-105. May 2015.
Perera, N., Dissanayake, H., Samson, D., Abeykoon, S., Jayathilaka, R., Jayasinghe, M., Yapa, S. “The interconnectedness of energy consumption with economic growth: A granger causality analysis”. Heliyon 10(17): e36709. September 2024.
Alola, A. A., Bekun, F. V., Sarkodie, S.A. “Dynamic impact of trade policy, economic growth, fertility rate, renewable and non-renewable energy consumption on ecological footprint in Europe”. Science of the Total Environment 685, pp. 702-709. October 2019.
Stern, D. I. “The role of energy in economic growth”. In “Ecological Economics Reviews”. Robert Costanza, Karin Limburg & Ida Kubiszewski, Editors. Annals of the New York Academy of Sciences 1219, pp. 26–51. February 2011.