There are thousands of cities in the world, each with its unique history. There are, nevertheless, regularities in how cities grow, which can be captured in the monocentric standard urban model (SUM). The SUM is also known as the Alonso-Muth-Mills model, named after a trio of works from the 1960s: Alonso (1964), Muth (1969), and Mills (1967).
Why Do We Have Cities?
In his 1967 paper, Mills (Mills (1967)) presents a simplified model that nevertheless helps to explain many common features of cities. That we have cities at all is something that is necessary to demonstrate. Mills assumes reasonably that most goods are produced, with the exception of land and labor, which are non-produced goods. If we assume that land is homogeneous–one acre is just as good as another for economic purposes–and if we assume constant returns to scale, then we should expect all people to spread out evenly to avoid bidding up land prices. In this scenario, there would be no cities.
First, land is clearly not homogeneous; some sites are more advantageous to certain industries than others. In particular, Mills notes that most major cities in the United States are located at strategic waterways to facilitate trade.
In Mills’ formulation, production of goods is a function of land, labor, and capital goods. The phrase constant returns to scale means that if the three inputs change by a certain percentage, then the output will change by the same percentage. More formally, Mills presents production of goods as follows.
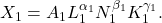
Here, X₁ is the total production of goods, A₁ is a constant, and the three factors respectively are land, labor, and capital. The constant returns to scale assumption is equivalent to α₁ + β₁ + γ₁ = 1. By 1967, the concept of agglomeration was already well-established and discussed by Mills. The most significant agglomeration economy is increasing returns to scale, which manifests itself mathematically as α₁ + β₁ + γ₁ > 1. We will have much more to say about agglomeration economies in a later article.
Another problem with the constant returns to scale assumption is indivisibility. Many goods and services are highly specialized with only niche markets, and thus a large population is necessary for the existence of firms to provide these products in an economically viable fashion. This is a framing of specialization, a major agglomeration economy.
For these reasons, cities exist, and Mills then concerns himself with explaining the structure of cities.
The Structure of Cities
A central business district (CBD) is taken to be the nucleus of a city. Monocentric means that there is a single CBD around which the city develops. Most large cities today are polycentric, meaning that there are several nuclei of economic activity. Mills assumes monocentricity for the sake of constructing a tractable model. As we shall see, despite this highly simplifying assumption, the monocentric SUM shows strong explanatory power.
Assuming that there are no geographic impediments to the expansion of the city, under the SUM a city is a series of concentric rings around the CBD. Each ring has a housing price and a land price, which decrease in the outer rings as they are offset by increase transportation costs to the CBD. Under the assumption of economic efficiency, housing costs plus transportation costs should be constant; otherwise people will move to where the sum of the two costs is lower. Here, transportation costs are not merely monetary, but also include the opportunity cost of the time spent traveling.
Transportation requires land and money, and different modes of transportation offer tradeoffs between these two costs. For example, Mills considers that subways require little land and much capital, while roads with personal automobiles requires much land and little capital. Which mode of transportation is favored depends on land prices. The SUM posits, and observation confirms, that subways will be more common where land is scarce and expensive.
Under the SUM, cities are surrounded by agricultural land with a nonzero price. The size of a city is set by the point at which value of land for outer suburbs is equal to the value for agricultural use.
Mills expresses the assumptions mathematically and obtains closed-form solutions for factors such as land prices and land use. He finds that for larger cities, a greater fraction of the land is needed for transportation. This fact too is observed in actual cities, and it serves as a constraint on the growth of cities. Interestingly, Mills does not find that large cities necessarily have heavy traffic congestion. Rather, unlike in the simplified model, in real life housing and workplaces cannot frictionlessly be converted into space for transportation, and the friction creates a shortage of transportation space for growing cities.
Mills finds that housing costs and population density both decrease with distance from the CBD, though in contrast to Clark (1951), Mills finds that these quantities fall at less than an exponential rate with distance.
Mills notes that Clark (1951) finds that transportation costs will result in a higher population density near the CBD and a lower density in the outer layers, but Mills points out that under his formulation, a change in transportation costs has an ambiguous effect on density overall.
Evaluating the SUM
The value of a mathematical model is not necessary found in how “true” it is–we have seem that the SUM as presented by Mills (1967) makes many simplifying assumptions–but rather in how well it helps us understand reality. Mills does not evaluate the model empirically in his paper, but many subsequent authors have, and despite the limitations, the SUM shows remarkable explanatory power.
Liotta, Viguié, and Lepetit (2022) conduct one of the most extensive empirical tests of the SUM. They construct a data set of 192 cities, representing every continent, though European cities are disproportionately represented. From various sources, they collect data on the spatial extent of the city, rent values, travel costs and times, gasoline prices, farmland prices, monocentricity, and stringency of land use regulation. Their findings largely confirm the predictions of the SUM.
Rent Gradients
It is well-known that in most cities, housing costs are higher when closer to the city center, and Liotta, Viguié, and Lepetit (2022) confirm that this pattern is common. Of 192 cities, the authors find that rents tend to decrease at locations farther from the city center in 167 cities; in 23 cities, the relationship between proximity to the CBD and rents was not significant at the 10% level; in one city–Riga, Latvia–rents were found to increase when farther from the city center; and in one city–Sfax, Tunisia–rental price data quality was not adequate enough to perform the analysis.
On average, a 1% increase in incomes net of transportation costs–both financial costs and the opportunity cost of the time commuting–corresponds with a 3.1% increase in rents, which is consistent with the observation that on average, citizens of OECD countries spend about a third of their income net of transportation on housing. However, the authors find that this elasticity varies considerably; most cities show an increase of 0% to 6% in rents for a 1% increase in incomes, but some cities show decreases, and some show increases above 8%.
Density Gradients
Liotta, Viguié, and Lepetit (2022) likewise confirm the prediction from the SUM that density tends to decrease at locations farther from the city center. All 192 cities show statistically significant decreases in density with distance from the center, though the rate of decrease varies considerably across cities. A 1% increase in transportation costs–again, “cost” is an aggregate of direct financial cost and the opportunity cost of commute time–was found to correlate with decreases in density ranging from 2.5% to 58.7%, with an average of 21.17%.
The observation of decreasing density gradients with distance from the CBD is well-known and has been observed as early as Clark (1951), well before the SUM had been articulated.
City Size
Under the SUM, the area of a city should increase with population and income, and it should decrease with farmland prices and transportation costs. Liotta, Viguié, and Lepetit (2022) confirm all four of these predictions.
The authors find that a 1% increase in population leads to a 0.86% increase in urban area, which also indicates a 0.14% increase in population density. A 1% increase in incomes leads to a 0.4% increase in urban area, indicating that higher incomes are used to increase per-capita land consumption. Higher farmland prices cause cities to be smaller, as it is more financially costly to acquire urban land at the periphery. Likewise, higher transportation costs cause cities to be smaller.
Under the SUM, higher fuel prices should also cause cities to be smaller for the same reason that higher transportation costs in general cause cities to be smaller. The authors are unable to confirm this claim, which they suggest is due to the fact that fuel prices are too noisy on time scales relevant to development of the built environment.
The Effect of Polycentricity
One limitation of Liotta, Viguié, and Lepetit (2022) is how they measure polycentricity, which recall is a measure of the number and geographic spread of employment centers in a city. The authors do include a measure of polycentricity based on how far apart five traditional measure of the city center are, but this definition does not capture the full significance of polycentricity as used by geographers.
Theory suggests that the density gradient should be smaller in a more polycentric city. In other words, the existence of many employment subcenters allow for many clusters of high density throughout the city, and they relieve some cross-city transportation demand, thus lowering transportation costs in the outer areas of the city and allowing greater density there. In addition to their limited polycentricity metric, the authors find that the density gradient tends to be lower in larger cities, which tend to be more polycentric. The authors hope that emerging machine learning approaches, such as employed by Barzin et al. (2022), will make polycentricity data more available for future research.
Nevertheless, Spivey (2008) examines cities in the United States, using Census data on population and housing and additional publicly available data on transportation and farmland costs. She finds that despite the increase in polycentricity in American cities up to 2000, as documented by McMillen and Smith’s (2003) analysis of commuting patterns, the SUM continues to hold explanatory powers on the urban form.
Conclusion
Mills (1967) himself admitted that the his urban model, which came to be known as the (monocentric) Standard Urban Model, has severe limitations. Perhaps the most serious limitation is the monocentricity assumption: the assumption that all employment occurs in the central business district and that all commuting occurs between residences and the CBD. Large cities have long been polycentric, with many distributed centers of employment, and as Spivey (2008) demonstrates, this is only becoming more true over time. Nevertheless, the SUM has shown remarkable robustness in explaining how cities develop.
Policymakers frequently seek to alter the structure of cities as it results from the SUM for a wide range of policy objectives, such as to preserve farm land, to contain urban sprawl, to limit urban population growth, to move transportation systems to preferred forms, and to reduce the need to travel. Given how widespread the urban form posited from the SUM are, across eras and regions, such policy objects should be pursued with care.
References
Alonso, W. Location and Land Use. Toward a General Theory of Land Rent. Cambridge: Harward University Press. 1964
Muth, R. F. Cities and Housing: The Spatial Pattern of Urban Residential Land Use. Chicago and London: The University of Chicago Press. 1969.
Mills, E. S. “An Aggregative Model of Resource Allocation in a Metropolitan Area”. The American Economic Review 57(2), Papers and Proceedings of the Seventy-ninth Annual Meeting of the American Economic Association, pp. 197-210. May 1967.
Clark, C. “Urban population densities”. Journal of the Royal Statistical Society, Series A (General), 114(4), pp. 490-496. 1951.
Liotta, C., Viguié, V., Lepetit, Q. “Testing the monocentric standard urban model in a global sample of cities”. Regional Science and Urban Economics 97: 103832. November 2022.
Barzin, S., Avner, P., Rentschler, J., O’Clery, N. “Where are All the Jobs? A Machine Learning Approach for High Resolution Urban Employment Prediction in Developing Countries”. Policy Research Working Paper 9979, World Bank, Washington, DC. March 2022.
Spivey, C. “The Mills–Muth Model of Urban Spatial Structure: Surviving the Test of Time?”. Urban Studies 45(2), pp. 295-312. February 2008.
McMillen, D.P., Smith, S.C. “The number of subcenters in large urban areas.”. Journal of urban economics 53(3), pp. 321-328. May 2003.